My web 1.1 indexer has been chugging away, though not like 24/7 or anything.


I mentioned this previously: keeping out the bad web isn't easy. Commercial links are everywhere and even the honest cases need scrutiny, e.g. a tech blog linking to Apache docs or something. This is particularly bad for SEO-minded sites that want to create outbound links for rank.

On the subject of wheat and chaff, to paraphrase:

Rob	Ick, why are there non-blog links in your recommendations?

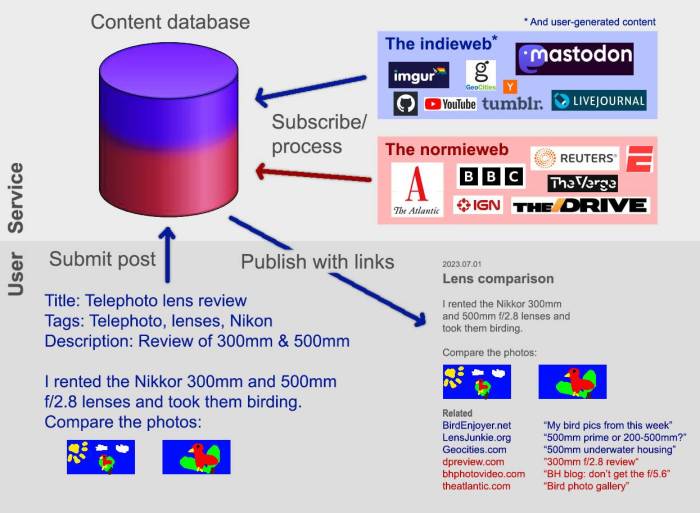
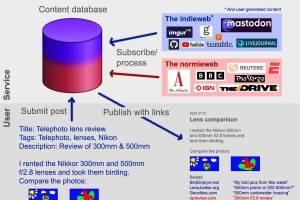
He's right, of course, I've often described this effort as linking the blogosphere, not the corposphere. Referring back to my original plan:

The bottom right illustrates a hypothetical post with external recommendations that are both indieweb (blue color scheme) and selective normieweb (red color scheme).

In the original design, each recommendation set would offer a handful of personal web links and a separate handful of mainstream links. I wasn't sure how to approach the latter other than: "The Atlantic, not Newsweek", "IGN, not Electronic Arts". I should come back to this quandary once I've fried some bigger fish.

Back when I had an experimental (small) post corpus I could quickly iterate over every indexed page. Searching for recommendations was quick despite the unmodest computational demands of trigram comparison with extra steps. As you might imagine, the post database eventually grew up and search began to take too long. At this point I could have pivoted to a vectorization/clustering approach but felt I could accomplish something similar with my existing trigram method. Recommendations were looking good, so why not stick with it?

The problem is a clustering one, though. Each post has a ranked list of similar post, though posts #2 and #3 might not be like each other. In thinking about search/recommendation, the vast majority of posts have nothing to do with the subject post, I really just want to consider the cluster.

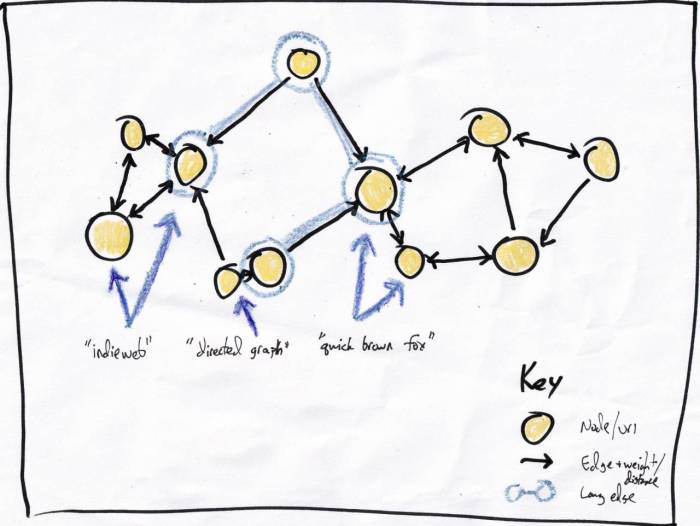
Since 50% of this project is therapeutic, I set out to create an iteration on my existing design rather than spend hours crawling github libraries. As opposed to the traditional clustering approach of mapping input to a point in n-dimensional space, I decided to treat each post as a node in a graph.


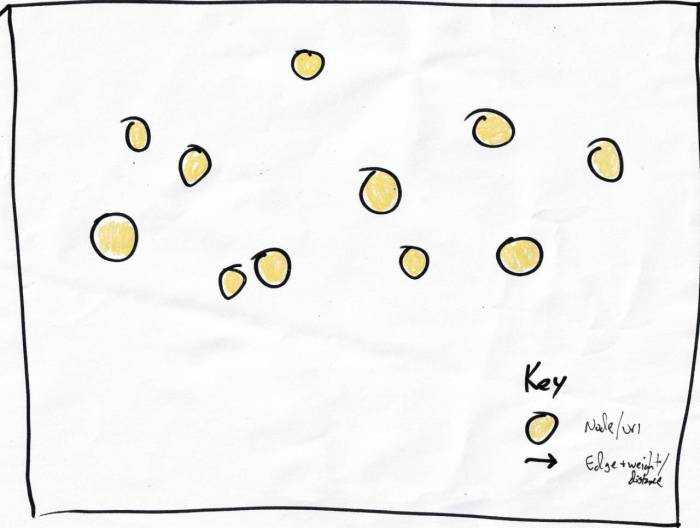
Simple enough, each yellow circle is a node/post.

The edges have lengths but I didn't write a number for them.

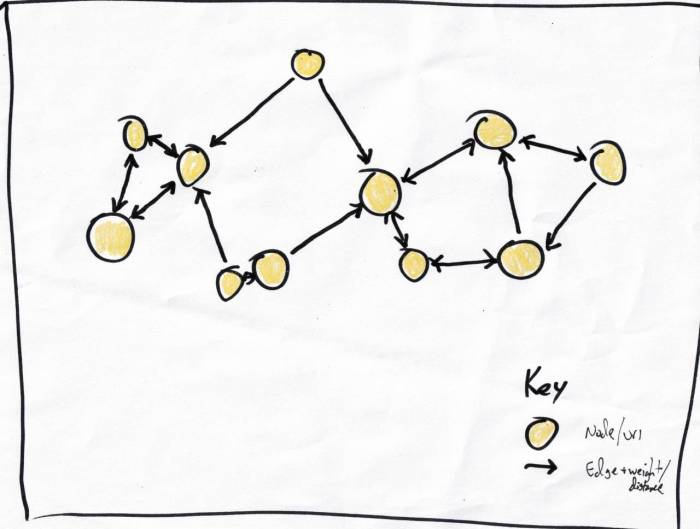
Each node can link to n nearest neighbors, nearness being determined by the trigram comparison algorithm. For simplicity I'm using n=2 in these napkin diagrams. The edges are directed but often form bidirectional links. This means:

• Everyone is connected to someone.
• This could form numerous unconnected subgraphs.

Building the graph was as simple as: for each node, traverse the entire graph and keep the closest n. This retraced the scalability issue that brought me here, but just once per page insert rather than every query.

For the objective of search/recommendation, I could examine connected clusters of nodes to find the recommendation candidates. And I could have a high degree of confidence that something 500 edges away was probably not worth considering.


Getting to those related clusters for an arbitrary post wasn't obvious. Often, with graphs, you'll have an entry node and traverse until you know you should stop. That's not the case here; if I'm looking for posts similar to footgolf (based on text content), is traversing from Yoshi's Island to ride-on lawnmowers a step in the right direction? The traversal needs to start in or near a cluster and there are often to multiple clusters if the subject post is about footgolf and electrical box paintings.

The search feels more like gradient descent. In short, if I delivered you via helicopter into the Sierra Nevadas and asked you to find the lowest point in a twenty-mile square, how would you proceed? You could walk downhill and find a low point, but you would need to traverse the entire 400 square miles to know it wasn't just a low-ish valley. Since the exhaustive approach is, well, exhausting, you might instead ask for a helicopter ride to a dozen points on the map, walk downhill, and then choose the lowest. And you'd be something like twelve times as confident as you would with just one descent.

Based on this view, I started tracking nodes that might provide a geographically-diverse span of the data. There might be a better way to accomplish this, but based on something Rob sent me, I assembled a list of entry points by recording nodes with the longest non-infinite edges. The search/recommendation process would still need to figure out how to best walk downhill, but this would give me a well-spaced set of starting points.


All this graph stuff was good but totally decoupled from the actual thing I was doing: comparing post text. What's more, if I selected 64 or 128 starting nodes to span the thousands or millions of webpages stored in the graph, these entry points could be unhelpful in plenty of situations.

Another idea I had kicked around before going the graph route was some sort of hierarchical trigram index. That seemed less fun to draw so I went with the graph approach, but a simple version of the index model could help here. I created an index of trigrams that appear between [small number] and [larger number] times in the entire corpus. Each index entry has pointers to the representative posts. It's a smallish, fast data structure that often points the search process in the right direction.


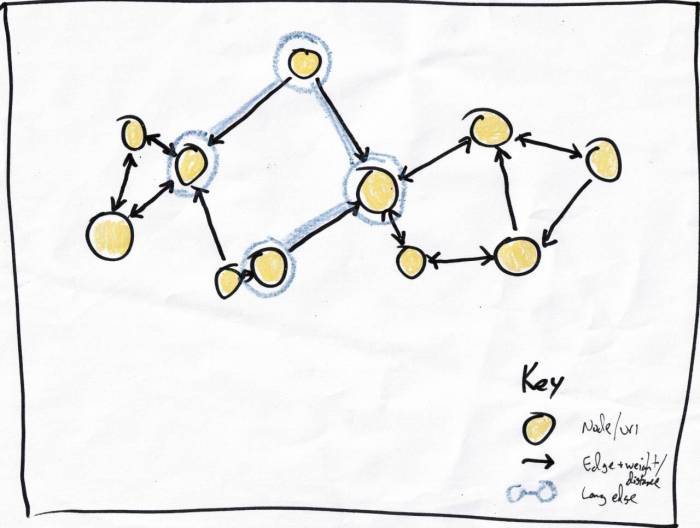
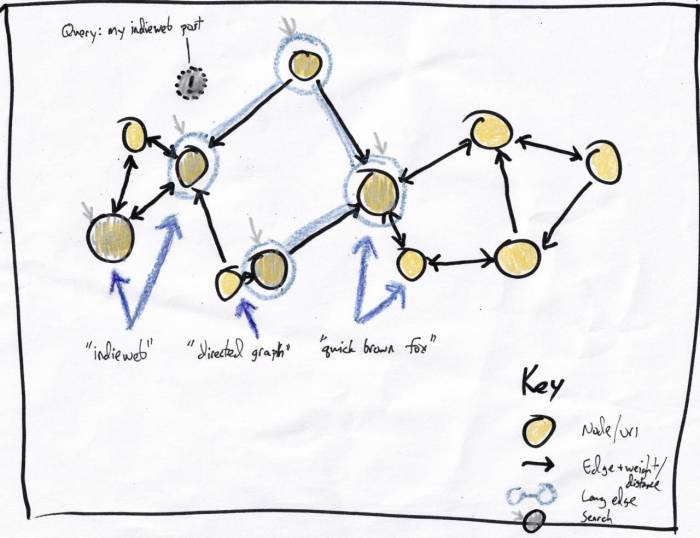
Back to my use case: finding recommendations for a post not contained in the graph. Illustrated above, the subject post is the (!) circle, my traversal starts with the gray arrows:

• The blue-circled nodes that are the default starting points based on having a long edge.
• The posts tracked in the index containing the term 'indieweb'.

The closest nodes to (!) are the would-be recommendations, you can see since it's a really small example I don't have to do too much work to get there from the starting nodes.


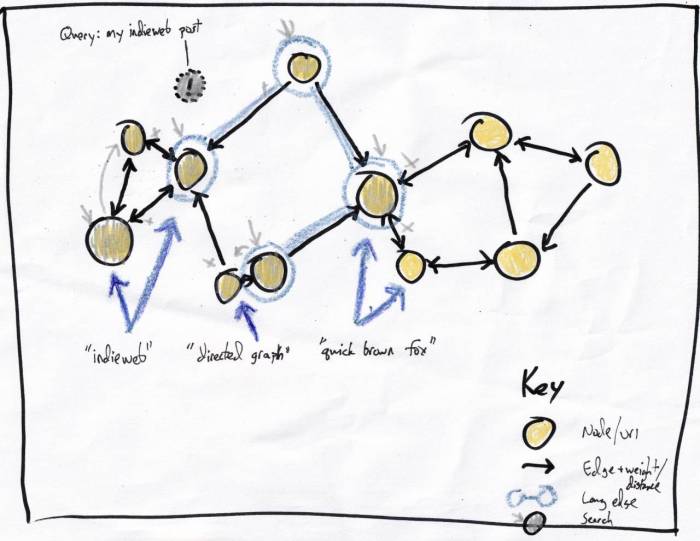
The traversal process is just a matter of checking adjacent, unvisited nodes and deciding whether to continue. Naively, I could just say, "keep going as long as the results are getting better". For (A)->(B), is the (!)/(B) similarity greater than the (!)/(A) similarity?

In the case illustrated above, the gray x's show traversals stopping, either because the node has already been visited or because the neighbor is less like the (!) node. Once traversal is finished, the algo has a list of visited nodes and their similarity to (!), analogous to the list of altitude measurements from the Sierras hike.

Related - internal

Related - external